
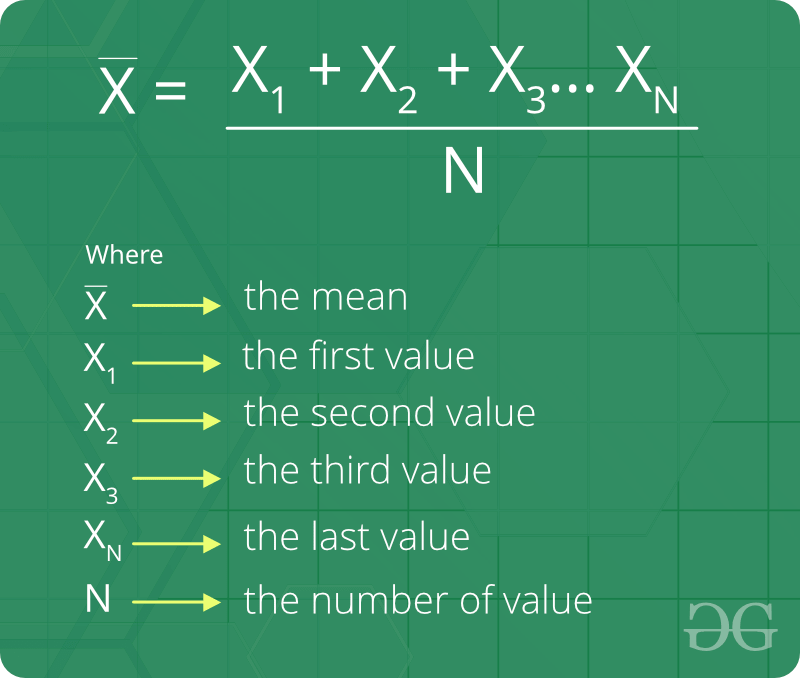
Jensen’s inequality generalizes the line segment definition we gave about the convex function.

So, if X is the convex subset of the real vector space and f : X → ℝ, then f is called convex if the following condition holds: for all 0 ≤ t ≤ 1 and x1, x2 ∈ X, f(tx1 + (1-t)x2) ≤ tf(x1) + (1 - t)f(x2).īy Eli Osherovich - Own work, CC BY-SA 3.0, įunctions like quadratic function (y = x²), exponential function (y = e^x), and negative logarithm function (y = -logx) are convex functions. But what is the convex function?Ī function is said to be convex if the line segment drawn using any two points of the curve is not below the curve between the two points. So, the convex loss functions in machine learning do not face the local minima problem. A strictly convex function in an open set has no more than one minimum. The convex function has convenient properties with respect to function optimization. The convex function plays a very important role in optimization. We will use this concept and Jensen’s inequality to establish the relationship between arithmetic mean and geometric mean. Let me introduce a mathematical concept here - the convex function. We will figure out later if there is such a relationship. A curious mind might wonder if this relationship is always true. We see geometric mean is less than the arithmetic mean. As the growth rates are evenly spaced, the arithmetic mean is the middle value i.e. In our population growth example, the geometric mean is 14.42% (rounded to two decimal places). If the values are a1, a2, a3, …, an, the geometric mean of the numbers is the nth root of the product of all the numbers. We might be happy to remember these evenly spaced three numbers but what if we have data for the last ten years? Is there any way to describe the population growth rate of the last n years with some average value? Yes, there is and that is where geometric mean comes. Suppose the annual population growth rate of Kathmandu, the capital city of Nepal, over the last three years is 10%, 15%, and 20%. This metric can be a descriptive measure to compare the performance of the players in the series. So, the arithmetic mean (or average) is 45.6. Here, the sum of all of the Smith’s scores is: 45 + 55 + 103 + 10 + 15 = 228. The arithmetic mean of some array of values is calculated by summing all the values and dividing the sum by the number of values. If we want to know how many runs Steve Smith scored per game, we can find that by calculating the arithmetic mean of his scores. In a 5-match ODI series, Steve Smith scored runs of 45, 55, 103, 10, and 15. Photo by Kate Bezzubets on Unsplash Arithmetic mean In analytics dashboards displaying web traffic and monetization information, we see average metrics like average CTR or average clicks mentioned all the time. When reading about global warming, we see the average rate of temperature rise being mentioned a lot. 96% efficacy of some COVID vaccine means 96 out of 100 people are prevented from infection on average, who otherwise would be infected. The efficacy of the COVID vaccines is interpreted as the mean value. Mean is not only important in our day-to-day use but also useful in academic and scientific research. In this article, we will discuss two types of mean - arithmetic mean and geometric mean. Be it inquiring about something, learning something, or asking something, we use it. AverageĪverage is at the heart of our life. In this article, we discuss two types of mean, interpret them using intuitive examples, introduce the convex function and Jensen’s inequality, and use them to establish the relationship between arithmetic mean and geometric mean.

So, it is important to grasp the concept of the mean from the ground up and be able to interpret it intuitively. The Bayesian viewpoint of linear regression says that the prediction is the mean of the posterior distribution. F1-score, one of the most important metrics when dealing with unbalanced data, is a harmonic mean of the two metrics - precision and recall. Arithmetic mean has a relationship with expectation. Mean is one of the most fundamental concepts in data science. Using Jensen’s inequality on logarithmic function to prove the relation between arithmetic and geometric mean Means in data science


 0 kommentar(er)
0 kommentar(er)
